Impulse (physics)

In classical mechanics, an impulse (abbreviated I or J) is defined as the integral of a force with respect to time. When a force is applied to a rigid body it changes the momentum of that body. A small force applied for a long time can produce the same momentum change as a large force applied briefly, because it is the product of the force and the time for which it is applied that is important. The impulse is equal to the change of momentum.

Impulse is the integral of force over time, it is measured in Newton-seconds. For instance a force of one Newton applied over one second will change the momentum, a force of two Newton's applied over half of a second will have a similar effect.
For rigid body collisions we take this to its limit and apply an infinite force over an infinitesimally small time. This impulse is equal to the change in momentum of the colliding objects. Because we are talking about forces here, Newton's third law applies, and the impulse on the colliding objects will be equal and opposite.
impulse = m(v_f- v_i)

where:		other definitions
symbol	description	type	units
J	impulse	vector	kg m/s
m	mass	scalar	kg
v_f	final velocity	vector	m/s
v_i	initial velocity	vector	m/s

This is the intergral of the inertia equation, F=ma.

Mathematical derivation in the case of an object of constant mass

Impulse I produced from time t₁ to t₂ is defined to be

$\mathbf{I} = \int_{t_1}^{t_2} \mathbf{F}\, dt$

where F is the force applied from

t 1

t 2

From Newton's second law, force is related to momentum p by

$\mathbf{F} = \frac{d\mathbf{p}}{dt}.$

Therefore

$\begin{align} \mathbf{I} &= \int_{t_1}^{t_2} \frac{d\mathbf{p}}{dt}\, dt \\ &= \int_{p_1}^{p_2} d\mathbf{p} \\ &= \Delta \mathbf{p}, \end{align}$

where Δp is the change in momentum from time t₁ to t₂. This is often called the impulse-momentum theorem.

As a result, an impulse may also be regarded as the change in momentum of an object to which a force is applied. The impulse may be expressed in a simpler form when both the force and the mass are constant:

$\mathbf{I} = \mathbf{F}\,\Delta t = m \,\Delta \mathbf{v} = \Delta\mathbf{p}$

where

F is the constant total net force applied,

Δt is the time interval over which the force is applied,

m is the constant mass of the object,

Δv is the change in velocity produced by the force in the considered time interval, and

Δp is the change in linear momentum.

It is often the case that not just one but both of these two quantities vary.

In the technical sense, impulse is a physical quantity, not an event or force. The term "impulse" is also used to refer to a fast-acting force. This type of impulse is often idealized so that the change in momentum produced by the force happens with no change in time. This sort of change is a step change, and is not physically possible. This is a useful model for computing the effects of ideal collisions (such as in game physics engines).

Impulse has the same units (in the International System of Units, kg·m/s = N·s) and dimensions (M L T⁻¹) as momentum.

Impulse can be calculated using the equation

$\mathbf{F}\,\Delta t = \Delta p = m\mathbf{v}_1 - m\mathbf{v}_0 \,$

where

F is the constant total net force applied,

t is the time interval over which the force is applied,

m is the constant mass of the object,

v₁ is the final velocity of the object at the end of the time interval, and

v₀ is the initial velocity of the object when the time interval begins.

Variable mass

When a system expels mass in one direction, the force the expelled mass applies to the system is called thrust; the force the system applies to the mass being expelled is of equal magnitude but opposite direction.

Consider for example a rocket. The momentum of the rocket (including the remaining fuel) changes due to two effects: one is the applied thrust, the other one is the reduction of mass:^[3]

dp = d(mv) = mdv + (dm)v = (dt)F + (dm)v = dI + (dm)v = (dm)v_e + (dm)v = (dm)(v_e + v)

where

p is the momentum of the rocket including the remaining fuel

dp is the infinitesimal change of the momentum of the rocket including the remaining fuel; it is the negative of the momentum of the mass being expelled, just after expulsion (the total momentum does not change)

m is the mass of the rocket including the remaining fuel (it decreases when mass is expelled)

dm is the infinitesimal change of the mass of the rocket including the remaining fuel, so the negative of the mass being expelled^[4]

v is the velocity of the rocket

v_e is the velocity of the just expelled mass relative to the rocket (effective exhaust velocity), hence:

v_e + v is the velocity of the just expelled mass

F is the thrust

dI is the infinitesimal impulse exerted on the rocket

Impulse and Newtons laws

Impulses have similar laws to forces (as they are time-intergral of force) so they happen in pairs (every impulse has an equal and opposite impulse) and they will be distributed through a framework in a similar way to forces.. Also any net impulse on an object will be ballanced by an impulse on the centre of mass of the object caused by inertia.

As an example, consider a snooker ball being hit off centre by a cue:

Table Top Physics - Snooker/pool - left side

A ball is hit by cue on the left, if we assume that the momentum is transferred only as an impulse, how do we work out the resulting linear and angular velocity of the ball?

Assume the following:

impulse = 1 kg m/s
mass of ball = 1 kg
radius of ball = r = 50 cm
offset of cue = 2/5 r² (chosen in hope of simplifying calculations, because this is the moment of inertia)

Method 1

linear velocity = impulse / mass = 1 m/s in the direction of the impulse

angular velocity = offset * impulse / I = (2/5 r²)/(2/5 r²) = 1 rad/sec clockwise

Method 2

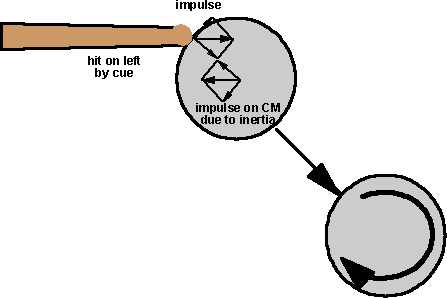In this method the impulse is resolved into a component toward the centre of mass and a component at 90 degrees, then assume that the component toward the CM generates the linear velocity and the component at 90 degrees generates the angular velocity.

Which is correct?

Can anyone help me here?

I think method 1 is correct because there is no justification for saying that the component toward the CM generates only the linear velocity and the component at 90 degrees generates only the angular velocity. However method 1 does not seem intuitively right, it seems that there should be some linear component to the right.

This is not a closed system so we cant use the conservation of angular momentum, is there a similar example which is a closed system, so that we can use conservation of angular momentum to check the result?

Calculating motion from impulse

Assume that we know the value of the impulse and we want to calculate the change in velocity. Note that when we know the initial velocity of the objects we may not know the impulse as described here.

Physics - Dynamics - Collision response

Here we are looking at the collision of rigid objects and how to calculate the response. There are a number of theoretical and practical issues that we need to consider, on this page we will start looking at the equations we get in collisions with combined rotation and linear motion, subpages look at the two and three dimensional cases in more detail. The way that momentum is transferred by an impulse is discussed on this page.

On this page we discuss more about the practical factors such as:

Whether we model the deformation of the objects or whether we assume solid body collisions.
What assumptions we make about elasticity coefficient and energy converted to heat.
What assumptions we make about friction and how objects slide.
How we handle multiple points of contact and simultaneous collisions.

There is no right answer to these questions, it depends on factors like: what we want to do, what accuracy do we need, how much computer power do we have, how stable must the simulation be and what type of materials are we dealing with.

Combined Rotation and Movement with a Linear Motion

It is difficult to analyse the situation when the colliding objects are free to both rotate and move with a linear motion. The main method we will use to do this involves the following stages.

Determine the collision point and the normal direction at this point.
Calculate the minimum impulse to prevent the objects intersecting, or to
reverse the approach velocity, depending on the coefficient of friction.
Calculate the effect of this impulse on the rotation and linear motion
separately.

This involves a lot of assumptions and approximations that may not always be valid, we need to understand what is going on to be sure that our simulations or programs are making the correct assumptions and that the results will be stable and accurate enough.

This method is based on the concept of an 'impulse' which is an instantaneous transfer of momentum between the objects. This is not intuitively obvious and I think its worth taking some time to rid ourselves of our natural misconceptions. The collision may involve an exchange of energy between the objects but the impulse is about momentum not energy, this distinction means:

Momentum is a vector quantity in which all the dimensions are independent and the linear dimensions are independent of the rotational dimensions.
Linear momentum and rotational momentum for a closed system are conserved independently, that is, linear momentum cannot be converted to rotational momentum and visa versa. Energy can be converted into other forms.
The component of momentum in each dimension for a closed system is conserved independently, that is, the x component of momentum cannot be converted to, or from, the y component of momentum. Again energy can be converted into other forms.
The whole of the impulse causes changes the linear momentum and rotational momentum, it is not that part of the impulse applies to linear momentum and the rest applies to rotational, all the impulse applies to both. In the case of energy we can ascribe part of the energy to the linear motion and another part to the rotational motion and energy can be transferred between them.

This last point is difficult for people to understand, it took me a long time for me to realise this and I have found that many other people have problems with it. This seems like something for nothing, the same impulse doing two jobs, but its not. The impulse just exchanges momentum between two objects and the same impulse can transfer the two types of momentum. Its not the same as energy and it works completely differently.

If you would like to see a practical example of this see this page (sent to me by Kevin Pegrume) which demonstrates this and highlights some of the counter intuitive issues.

Results

Here are equations for calculating the components of impulse (J) then the equations to use this to calculate the new velocities. This is just an overview, the definitions and derivations are given on the individual pages for the one, two and three cases:

The results for the one dimensional case (no rotation) are as follows: (see this page for code and derivation)

	General Case (between Perfectly elastic and Perfectly inelastic)
coefficient of restitution	e = (- ) / ( - )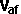
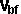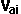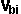impulse =	(e+1)(- )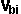
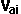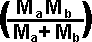
Final velocity of object a= 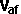=	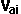* 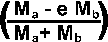+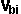(e+1)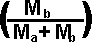
Final velocity of object b= 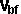=	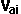(e+1) +

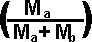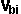
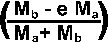The results for the two dimensional case are as follows: (see this page for code and derivation)

	General Case (between Perfectly elastic and Perfectly inelastic)
impulse =	Jx = (e+1)/k * (Vaix - Vbix)( 1/ma - rax²/Ia + 1/mb - rbx²/Ib) - (e+1)/k * (Vaiy - Vbiy) (rax ray / Ia + rbx rby / Ib) Jy = - (e+1)/k * (Vaix - Vbix) (rax ray / Ia + rbx rby / Ib) + (e+1)/k * (Vaiy - Vbiy) ( 1/ma - ray²/Ia + 1/mb - rby²/Ib) where: k=1/ma²+ 2/ma mb +1/mb² - rax²/maIa - rbx²/maIb - ray²/maIa - ray²/mbIa - rax²/mbIa - rbx²/mbIb - rby²/maIb - rby²/mbIb + ray²rbx²/IaIb + rax² rby²/IaIb - 2 rax ray rbx rby/IaIb
Final velocity of object a=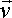_af =	Vaix - Jx/Ma Vaiy - Jy/Ma
Final velocity of object b=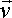_bf =	Vbix - Jx/Mb Vbiy - Jy/Mb
Final angular velocity of object a=w_af =	waix - (Jx ray - Jy rax) /I waiy - (Jx ray - Jy rax) /I
Final angular velocity of object b=w_bf =	wbix - (Jx rby - Jy rbx) /I wbiy - (Jx rby - Jy rbx) /I

The results for the three dimensional case are as follows: (see this page for code and derivation)

General Case (between Perfectly elastic and Perfectly inelastic)

impulse J =

-(1+e)	(v_a-v_b)•n + (r_a×n)•ω_a - (r_b×n)•ω_b

	1/m_a+1/m_b+(ra×n)•([I_a]^-1(r_a×n))+(r_b×n)•([I_b]^-1(r_b×n))

Final velocity of object a=

_af =

Vai - J/Ma

Final velocity of object b=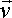

_bf =

Vbi - J/Mb

Final angular velocity of object a=w_af =

wai - [Ia]^-1(J x ra)

Final angular velocity of object b=w_bf=

wbi - [Ib]^-1(J x rb)

Collision Response for unconstrained rigid bodies

Until now we have kept the rotation and linear components separate, it would be good if we could combine them into a single set of equations, I can think of two approaches: here we combine them using vectors and matrices. I would also like to try an approach using geometric algebra andconformal space but I have not made any progress with yet.

As already explained here, When unconstrained rigid bodies are floating round in free space, perhaps under the influence of forces, then each object might be represented by a state vector like the following:

Dynamics state vector for an object:

θx

θy

θz

mvx

mvy

mvz

These values might be gradually changing with time in a way that can be described by simple linear equations. This would go on until two or more objects collide, this produces a step change in these variables, a discontinuity or singularity, when an impulse is transferred between the two objects in an infinitesimally small time. When such a collision occurs we need to calculate the new state vectors for each object. To do this we need to gather the following information which describes the collision:

Collision parameters:

reference to object a

reference to object b

sva

state vector for object a - 12 dimensional vector as above

svb

state vector for object b - 12 dimensional vector as above

Newton-Euler matrix for object a

iaxx	iaxy	iaxz	0	-haz	hay
iayx	iayy	iayz	haz	0	-hax
iazx	iazy	iazz	-hay	hax	0
0	haz	-hay	ma	0	0
-haz	0	hax	0	ma	0
hay	-hax	0	0	0	ma

This matrix is explaind here and combines the following information:

mass of object a
Inertia Tensor for object a (in the global coordinate system - so needs to be computed at the time of the collision)
offset of the point of collision from the centre of mass of object a - also needs to be calculated at the time of collision.

Newton-Euler matrix for object b

ibxx	ibxy	ibxz	0	-hbz	hby
ibyx	ibyy	ibyz	hbz	0	-hbx
ibzx	ibzy	ibzz	-hby	hbx	0
0	hbz	-hby	mb	0	0
-hbz	0	hbx	0	Mb	0
hby	-hbx	0	0	0	Mb

As above for object b

A normal vector (dimension 3), this is a normal to the point of collision and shows the direction that the impulse is transferred.

cfa, cfb

Optional coefficient of friction for each object

Physics Assumptions

The following is an analytical approach to collisions, it assumes the collision occurs at a point contact between rigid objects. This means that the objects do not break or deform on collision. If these assumptions would cause too many errors, for instance modeling the deformations of a car in a crash, or if the analytical approach produces equations which are too complex then try a numerical approach to collisions.

The dynamics equations for a single object were covered in the previous page. Here we extend this analysis to two objects so that we can calculate the result of a collision between the objects. As explained in the previous page, we need to translate all values (inertia, force, movement, etc.) to world or common coordinates.

Linear momentum, angular momentum and energy is passed between the colliding shapes at the point of collision by means of impulse. Assuming that we know the velocities before the impact, and the point of impact, then one or more of the following might be used to help us calculate the velocities after the collision:

Conservation of momentum - The total momentum of the whole system will be conserved. The momentum is a vector quantity so in the 3D case it is conserved in whatever x,y and z axis we choose.
Conservation of energy - The total energy of the whole system will be conserved, but energy may be converted between kinetic energy and other types of energy. So we need to make assumptions about this. In a perfectly elastic collision then the kinetic energy is conserved, in an inelastic collision some of the energy associated with the approaching objects may be converted to heat.
Calculation of Impulse - The impulse could be calculated which would allow us to work out the change in velocity of both objects.

Also there are different outcomes depending on the properties of the objects colliding:

If the objects are perfectly elastic, they will absorb the kinetic energy of the collision as potential energy (like a spring) and then instantly convert it back to kinetic energy, so that the objects bounce off each other with a separating velocity equal and opposite to the approaching velocity.
If the objects are perfectly inelastic, they will stick together and the final velocities of the two objects will be equal. In this case the total kinetic energy will be reduced and some energy will be converted into heat or other forms of energy.
The objects may be somewhere in-between these two extremes. So we could introduce an elasticity factor for each colliding object which would give final velocities somewhere between these two extremes. Another complication is that this factor might be different in different dimensions, for instance objects may collide and slide against each other, so friction may also need to be taken into account.

Other concepts:

Impulse is the integral of force over time, it is measured in Newton-seconds. For instance a force of one Newton applied over one second will change the momentum, a force of two Newton's applied over half of a second will have the same effect. For rigid body collisions we take this to its limit and apply an infinite force over an infinitesimally small time. This impulse is equal to the change in momentum of the colliding objects. Because we are talking about forces here, Newton's third law applies, and the impulse on the colliding objects will be equal and opposite.

Rotation
Once we start working in two and three dimensions, there is the possibility of rotation to include. This makes the general solution of a collision very difficult to work out (too difficult for me so far - but I'm working on it, can you help?). Rotation has similar laws to linear collisions, there are equivalents to Newtons laws for rotations and the total angular momentum of a system is conserved in the same way as linear momentum is conserved. However the following issues make the calculation of collision response difficult:

Lots more variables. In 3 dimensions there are 12 degrees of freedom, i.e. 12 variables to calculate, 3 linear for each object and 3 angular for each object.
When working with linear values in a Newtonian system there is a principal of 'relativity', i.e. velocities are measured relative to something else, or to put it another way, the frame of reference can be set relative to any of the objects in the system and all the rules will work correctly. In fact there are no absolute velocities, no frame of reference is better than any other. So we can travel on one of the traveling objects and calculate the response of the colliding object relative to it. In the case of a system with rotation then, there is an absolute frame of reference for rotation, this is the frame of reference where objects, with no forces acting on them, travel in straight lines. Otherwise, if we have a rotating frame of reference, say from the point of view of a person standing on a rotating planet will see a colliding object appearing to travel in a spiral. So Newtons laws do not appear to work in a rotating frame of reference.
There are other complications in a system of mixed linear and rotational movements, for example, the resultant velocities depend on the point of impact, i.e. have the objects collided head on, or is it a glancing collision.

Friction
In a complicated collision, then friction may be involved. However friction (as opposed to elasticity) is only involved if there is a force, such as gravity, pushing the colliding objects together.

Collisions in 3 dimensions is quite a complex problem, I'll start with 1 dimension first, then try to build up to 2 and then 3 dimensions.

Rigid Body Collisions - deriving general equations
Rigid Body Collisions - numerical solution
collisions with deformations

Implementing this in program

One issue I would like to keep in mind through these pages is, how do we use this theory in the program? It is proposed to include information about these physical properties in the scene graph.

For information about how to use this in the program see dynamics tutorial.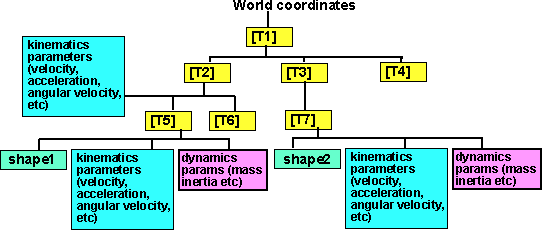

Determining the impact point

We not only need to detect that there has been a collision, we also need to find the point of impact relative to the centres of mass so that we can pass this information on to the collision response system.

We want to calculate the motion of the rigid body after the impulse as the sum of the linear motion of its centre of mass and its rotation about its centre of mass.

Linear motion

I think its linear motion is simple, since F = ma = m dv/dt this gives:

Change in velocity = dv = (F/m) dt = impulse/m

So the linear motion will be in the same direction as the impulse, even if the impulse is applied at a point offset from the centre of mass, this seems counter intuitive and this is what I have been trying to get to grips with in the various examples on the website. I think the is correct however, I think that this does not correspond to our intuition because in a practical collision the impulse is not necessarily in the direction of the impact but will have a component which is normal to the surface of the colliding objects.

Rotation motion

I think we could have an equivalent to Newtons 3^rd law for impulses, in other words: every impulse has an equal and opposite impulse. If we apply the impulse to an object which is not attached to anything else then I think this equal and opposite reaction would act on the centre of mass.

Perhaps we could have an angular equivalent of impulse as follows:

Linear impulse = integral(Force) dt = change of linear momentum

Angular impulse = integral(Torque) dt = change of angular momentum

However I think we have to be careful here because in the linear case:

F=ma where m=mass which is a scalar quantity

but in the angular case we have:

T = [I] angAcc where [I] = inertia tensor which is a 3x3 matrix in global coordinates (which will change as the object rotates)

So is it valid to say that:

Change in angular velocity = [I]^-1 angular impulse

where:		other definitions
symbol	description	type	units
[I]^-1	the inverse of the inertia tensor in global coordinates (which will change as the object rotates)	matrix
angular impulse	Linear impulse × d	bivector
d	distance between c of m and point where impulse is applied	vector	m
×	vector cross product
Linear impulse		vector

6 x 6 Matrix representation

So, in the same way that we did for the inertia equation, we can represent the 3D case

impRot_x

impRot_y

impRot_z

impx

impy

impz

ixx	ixy	ixz	0	-hz	hy
iyx	iyy	iyz	hz	0	-hx
izx	izy	izz	-hy	hx	0
0	hz	-hy	m	0	0
-hz	0	hx	0	m	0
hy	-hx	0	0	0	m

w_xf-w_xi

w_yf-w_yi

w_zf-w_zi

vxf-vxi

vyf-vyi

vzf-vzi

where:		other definitions
symbol	description	type	units
ixx ... izz	inerta moment components
w_xf,w_yf,w_zf	final rotation velocity components	bivector
w_xi,w_yi,w_zi	initial rotation velocity components	bivector
vxf,vyf,vzf	final linear velocity components	vector
vxi,vyi,vzi	initial linear velocity components	vector
m	mass	scalar
hx, hy, hz	sxm, sym, sz*m
impx, impy, impz	linear impulse
impRotx, impRoty, impRotz	rotational impulse

Impulse with Examples

In summary, I try to say that impulse is the multiplication of applied force and time interval it applied. Impulse is also a vector quantity having both magnitude and direction. It has the same direction with applied net force.

Impulse=Force.Time Interval

Impulse and momentum are directly related to each other. Let’s find this relation now.

As you can see, we found that impulse is equal to the change in momentum. In examples we will benefit from this equation.

Impulse=Change in Momentum

Example If the time of force application is 5s find the impulse of the box given below.

Impulse=Force.Time Interval

Impulse=15N.5s

Impulse=75N.s

Example Find applied force which makes 10m/s change in the velocity of the box in 5s if the mass of the box is 4kg.

Impulse=Change in momentum

F.t=p₂-p₁

F.t=m. (V₂-V₁)

F.t=4kg.10m/s=40kg.m/s Impulse of the box is 40kgm/s

F=40kg.m/s/5s=8N Applied force

We experience the results of impulse and momentum in daily life. For example, in collisions like car crash or any other collision we can calculate the affect of force by controlling the time. Assume that, you push a box with a force of 10N for 2 seconds, the impulse is 20N.s. Then you push it with a 5N force for 4 seconds and impulse does not change. As you see increasing the time decreases the amount of force. Thus, the unwanted results of force can be eliminated by increasing the time of force application. On the contrary if you want big force then you should decrease the time and you get big force.

In this unit we will again benefit from the graphs. Look at the given graph below that shows the relationship of the force and time of a given system.

Since impulse is equal to the multiplication of force and time then, area under this graph also gives us impulse. As shown in the graph, A1 is positive impulse and A2 is negative impulse. Total impulse gives us the change in momentum as we said before.

We can also draw momentum versus time and velocity versus time graph of the system.

As you can see momentum vs. time graph and velocity vs. time graphs of the system are similar because momentum is directly proportional to the velocity.

Example The graph given below belongs to an object having mass 2kg and velocity 10m/s. It moves on a horizontal surface. If a force is applied to this object between (1-7) seconds find the velocity of the object at 7. Second.

Area under the graph gives us impulse. First, we find the total impulse with the help of graph given above then total impulse gives us the momentum change. Finally, we find the final velocity of the object from the momentum change.

Momentum

In classical mechanics, momentum (pl. momenta; SI unit kg·m/s, or, equivalently, N·s) is the product of the mass and velocity of an object ( $\mathbf{p} = m\mathbf{v}$ ). Like velocity, momentum is a vector quantity, possessing a direction as well as a magnitude. Momentum is a conserved quantity (law of conservation of linear momentum), meaning that if a closed system is not affected by external forces, its total momentum cannot change. Momentum is sometimes referred to as linear momentum to distinguish it from the related subject of angular momentum.

Although originally expressed in Newton's Second Law, the conservation of momentum also holds in special relativity and, with appropriate definitions, a (generalized) momentum conservation law holds in electrodynamics, quantum mechanics, quantum field theory, and general relativity. In relativistic mechanics, non-relativistic momentum is further multiplied by the Lorentz factor.

Linear momentum of a particle

Newton's apple in Einstein's elevator. In person A's frame of reference, the apple has non-zero velocity and momentum. In the elevator's and person B's frames of reference, it has zero velocity and momentum.

If an object is moving in any reference frame, then it has momentum in that frame. It is important to note that momentum is frame dependent. That is, the same object may have a certain momentum in one frame of reference, but a different amount in another frame. For example, a moving object has momentum in a reference frame fixed to a spot on the ground, while at the same time having 0 momentum in a reference frame attached to the object's center of mass.

The amount of momentum that an object has depends on two physical quantities: the mass and the velocity of the moving object in the frame of reference. In physics, the usual symbol for momentum is a bold p (bold because it is a vector); so this can be written

$\mathbf{p}= m \mathbf{v}\,,$

where p is the momentum, m is the mass and v is the velocity.

Example: a model airplane of 1 kg traveling due north at 1 m/s in straight and level flight has a momentum of 1 kg·m/s due north measured from the ground. To the dummy pilot in the cockpit it has a velocity and momentum of zero.

According to Newton's second law, the rate of change of the momentum of a particle is proportional to the resultant force acting on the particle and is in the direction of that force. The derivation of force from momentum is given below.

$\sum{\mathbf{F}} = {\mathrm{d}\mathbf{p} \over \mathrm{d}t} = m{\mathrm{d}\mathbf{v} \over \mathrm{d}t} + \mathbf{v}{\mathrm{d}m \over \mathrm{d}t}$

Given that mass is constant, the second term of the derivative is zero ( $\scriptstyle \mathbf{v}{\mathrm{d}m \over \mathrm{d}t} = 0$ ). We can therefore write the following:

$\sum{\mathbf{F}} = m\mathbf{a}\,$

or just simply

$\mathbf{F}= m \mathbf{a}\,,$

where F is understood to be the net force (or resultant).

Example: a model airplane of 1 kg accelerates from rest to a velocity of 1 m/s due north in 1 s. The thrust required to produce this acceleration is 1 newton. The change in momentum is 1 kg·m/s. To the dummy pilot in the cockpit there is no change of momentum. Its pressing backward in the seat is a reaction to the unbalanced thrust, shortly to be balanced by the drag.

Linear momentum of a system of particles

Relating to mass and velocity

The linear momentum of a system of particles is the vector sum of the momenta of all the individual objects in the system:

$\mathbf{p}= \sum_{i = 1}^n m_i \mathbf{v}_i = m_1 \mathbf{v}_1 + m_2 \mathbf{v}_2 + m_3 \mathbf{v}_3 + \cdots + m_n \mathbf{v}_n\,,$

where p is the total momentum of the particle system, m_i and v_i are the respective mass and velocity of the i-th object, and n is the number of objects in the system.

It can be shown that, in the center of mass frame the momentum of a system is zero. Additionally, the momentum in a frame of reference that is moving at a velocity v_cm with respect to that frame is simply:

$\mathbf{p}= m\mathbf{v}_\text{cm}\,,$

where:

$m=\sum_{i = 1}^n m_i\,.$

This is known as Euler's first law.

Relating to force – General equations of motion

Motion of a material body

The linear momentum of a system of particles can also be defined as the product of the total mass, m, of the system times the velocity,v_cm, of the center of mass.

$\sum{\mathbf{F}} = {\mathrm{d}\mathbf{p} \over \mathrm{d}t}= m \frac{\mathrm{d}\mathbf{v}_{cm}}{\mathrm{d}t}=m\mathbf{a}_{cm}\,$

This is a special case of Newton's second law (if mass is constant).

For a more general derivation using tensors, we consider a moving body (see Figure), assumed as a continuum, occupying a volume V, at a time t, having a surface area S, with defined traction or surface forces per unit area represented by the stress vector $\scriptstyle T_i^{(n)}\,$ acting on every point of every body surface (external and internal), body forces F_i per unit of volume on every point within the volume V, and a velocity field v_i, prescribed throughout the body. Following the previous equation, the linear momentum of the system is:

$\int_S T_i^{(n)}dS + \int_V F_i dV = \frac{d}{dt}\int_V \rho\, v_i\, dV\,.$

By definition the stress vector is defined as $\scriptstyle T_i^{(n)} \equiv \sigma_{ij}n_j\,$ , then

$\int_S \sigma_{ij}n_j\, dS + \int_V F_i\, dV = \frac{d}{dt}\int_V \rho\, v_i\, dV\,.$

Using the Gauss's divergence theorem to convert a surface integral to a volume integral gives (we denote $\scriptstyle \partial_j \equiv \frac{\partial}{\partial x_j}\,$ as the differential operator):

$\int_V \partial_j\sigma_{ij}\, dV + \int_V F_i\, dV = \frac{d}{dt}\int_V \rho\,v_i\, dV\,.$

Now we only need to take care of the right side of the equation. We have to be careful, since we cannot just take the differential operator under the integral. This is because while the motion of the continuum body is taking place (the body is not necessarily solid), the volume we are integrating on can change with time too. So the above integral will be:

$\frac{d}{dt}\int \rho\,v_i\, dV=\int \frac{\partial (\rho v_i)}{\partial t}\, dV +\oint \rho v_i v_k n_k dA\,.$

Performing the differentiation in the first part, and applying the divergence theorem on the second part we obtain:

$\frac{d}{dt}\int \rho\,v_i\, dV =\int \left[ \left(\rho\frac{\partial v_i}{\partial t}+v_i\frac{\partial \rho}{\partial t}\right)+\partial_k (\rho v_i v_k)\right]\, dV\,.$

Now the second term inside the integral is: $\partial_k (\rho v_i v_k)=\rho v_k \cdot \partial_k v_i +v_i\partial_k(\rho v_k)\,.$ Plugging this into the previous equation, and rearranging the terms, we get:

$\frac{d}{dt}\int \rho\,v_i\, dV=\int\rho\left[\frac{\partial}{\partial t}+v_k\partial_k\right]v_i\,dV +\int\left[\frac{\partial\rho}{\partial t}+\partial_k(\rho v_k)\right]v_i\,dV\,.$

We can easily recognize the two integral terms in the above equation. The first integral contains the convective derivative of the velocity vector, and the second integral contains the change and flow of mass in time. Now lets assume that there are no sinks and sources in the system, that is mass is conserved, so this term is zero. Hence we obtain:

$\frac{d}{dt}\int \rho\,v_i\, dV=\int \rho\,\frac{Dv_i}{Dt}\, dV\,$

putting this back into the original equation:

$\int_V \left[ \partial_j\sigma_{ij} + F_i - \rho \frac{D v_i}{Dt}\right]\, dV = 0\,.$

For an arbitrary volume the integrand itself must be zero, and we have the Cauchy's equation of motion

$\partial_j\sigma_{ij} + F_i = \rho \frac{D v_i}{Dt}\,.$

As we see the only extra assumption we made is that the system doesn't contain any mass sources or sinks, which means that mass is conserved. So this equation is valid for the motion of any continuum, even for that of fluids. If we are examining elastic continua only then the second term of the convective derivative operator can be neglected, and we are left with the usual time derivative, of the velocity field.

If a system is in equilibrium, the change in momentum with respect to time is equal to 0, as there is no acceleration

$\sum{\mathbf{F}} = {\mathrm{d}\mathbf{p} \over \mathrm{d}t}=\ m\mathbf{a}_{cm}= 0\,$

or using tensors,

$\partial_j\sigma_{ij} + F_i = 0\,.$

These are the equilibrium equations which are used in solid mechanics for solving problems of linear elasticity. In engineering notation, the equilibrium equations are expressed in Cartesian coordinates as

$\frac{\partial \sigma_x}{\partial x} + \frac{\partial \tau_{yx}}{\partial y} + \frac{\partial \tau_{zx}}{\partial z} + F_x = 0\,$

$\frac{\partial \tau_{xy}}{\partial x} + \frac{\partial \sigma_y}{\partial y} + \frac{\partial \tau_{zy}}{\partial z} + F_y = 0\,$

$\frac{\partial \tau_{xz}}{\partial x} + \frac{\partial \tau_{yz}}{\partial y} + \frac{\partial \sigma_z}{\partial z} + F_z = 0\,.$

Conservation of linear momentum

This example (m1 = 4kg, u1 = 5m/s, m2 = 4kg, u2=0m/s) of collision carts in perfectly inelastic collision, notice the center of mass of the masses m1 and m2 is at the location of vcm = 2.5m/s always throughout the motion.

The law of conservation of linear momentum is a fundamental law of nature, and it states that if no external force acts on a closed system of objects, the momentum of the closed system remains constant. One of the consequences of this is that the center of mass of any system ofobjects will always continue with the same velocity unless acted on by a force from outside the system.

Conservation of momentum is a mathematical consequence of the homogeneity (shift symmetry) of space (position in space is the canonical conjugate quantity to momentum). That is, conservation of momentum is equivalent to the fact that the physical laws do not depend on position.

In analytical mechanics the conservation of momentum is a consequence of translational invariance of Lagrangian in the absence of external forces. It can be proven that the total momentum is a constant of motion by making an infinitesimal translation of Lagrangian and then equating it with non translated Lagrangian. This is a special case of Noether's theorem .

In an isolated system (one where external forces are absent) the total momentum will be constant: this is implied by Newton's first law of motion. Newton's third law of motion, the law of reciprocal actions, which dictates that the forces acting between systems are equal in magnitude, but opposite in sign, is due to the conservation of momentum.

Since position in space is a vector quantity, momentum (being the canonical conjugate of position) is a vector quantity as well—it has direction. Thus, when a gun is fired, the final total momentum of the system (the gun and the bullet) is the vector sum of the momenta of these two objects. Assuming that the gun and bullet were at rest prior to firing (meaning the initial momentum of the system was zero), the final total momentum must also equal 0.

In an isolated system with only two objects, the change in momentum of one object must be equal and opposite to the change in momentum of the other object. Mathematically,

$\Delta \mathbf{p}_1 = -\Delta \mathbf{p}_2\,.$

Momentum has the special property that, in a closed system, it is always conserved, even in collisions and separations caused by explosive forces. Kinetic energy, on the other hand, is not conserved in collisions if they are inelastic. Since momentum is conserved it can be used to calculate an unknown velocity following a collision or a separation if all the other masses and velocities are known.

A common problem in physics that requires the use of this fact is the collision of two particles. Since momentum is always conserved, the sum of the momenta before the collision must equal the sum of the momenta after the collision:

$m_1 \mathbf u_{1} + m_2 \mathbf u_{2} = m_1 \mathbf v_{1} + m_2 \mathbf v_{2}\,,$

where u₁ and u₂ are the velocities before collision, and v₁ and v₂ are the velocities after collision.

Determining the final velocities from the initial velocities (and vice versa) depend on the type of collision. There are two types of collisions that conserve momentum: elastic collisions, which also conserve kinetic energy, and inelastic collisions, which do not.

Elastic collisions

Example (m1 = 4kg, u1 = 5m/s, m2 = 4kg, u2=0m/s) of collision carts in perfectly elastic collision showing the equations of momentum and kinetic energy both conserved

A collision between two pool balls is a good example of an almost totally elastic collision, due to their high rigidity; a totally elastic collision exists only in theory, occurring between bodies with mathematically infinite rigidity. In addition to momentum being conserved when the two balls collide, the sum of kinetic energy before a collision must equal the sum of kinetic energy after:

$\tfrac{1}{2} m_1 u_{1}^2 + \tfrac{1}{2} m_2 u_{2}^2 = \tfrac{1}{2} m_1 v_{1}^2 + \tfrac{1}{2} m_2 v_{2}^2\,.$

In one dimension

When the initial velocities are known, the final velocities for a head-on collision are given by

$\mathbf{v}_{1} = \left( \frac{m_1 - m_2}{m_1 + m_2} \right) \mathbf{u}_{1} + \left( \frac{2 m_2}{m_1 + m_2} \right) \mathbf{u}_{2}\,$

$\mathbf{v}_{2} = \left( \frac{m_2 - m_1}{m_1 + m_2} \right) \mathbf{u}_{2} + \left( \frac{2 m_1}{m_1 + m_2} \right) \mathbf{u}_{1}\,.$

This example m1=1000kg, u1=5m/s, m2=0.1kg, u2=0m/s, the final velocities are approximately given v1=4.999m/s, v2=9.999m/s

When the first body is much more massive than the other (that is, m₁ » m₂), the final velocities are approximately given by

$\mathbf{v}_{1} = \mathbf{u}_{1}\,$

$\mathbf{v}_{2} = 2\mathbf{u}_{1} - \mathbf{u}_{2}\,.$

Thus the more massive body does not change its velocity, and the less massive body travels at twice the velocity of the more massive body less its own original velocity. Assuming both masses were heading towards each other on impact, the less massive body is now therefore moving in the opposite direction at twice the speed of the more massive body plus its own original speed.

A Newton's cradle demonstrates conservation of momentum.

In a head-on collision between two bodies of equal mass (that is, m₁ = m₂), the final velocities are given by

$\mathbf{v}_1 = \mathbf{u}_2\,$

$\mathbf{v}_2 = \mathbf{u}_1\,.$

Thus the bodies simply exchange velocities. If the first body has nonzero initial velocity u₁ and the second body is at rest, then after collision the first body will be at rest and the second body will travel with velocity u₁. This phenomenon is demonstrated by Newton's cradle.

In multiple dimensions

In the case of objects colliding in more than one dimension, as in oblique collisions, the velocity is resolved into orthogonal components with one component perpendicular to the plane of collision and the other component or components in the plane of collision. The velocity components in the plane of collision remain unchanged, while the velocity perpendicular to the plane of collision is calculated in the same way as the one-dimensional case.

For example, in a two-dimensional collision, the momenta can be resolved into x and y components. We can then calculate each component separately, and combine them to produce a vector result. The magnitude of this vector is the final momentum of the isolated system.

Perfectly inelastic collisions

Example (m1 = 4kg, u1 = 5m/s, m2 = 4kg, u2=0m/s) of collision carts in perfectly inelastic collision showing the equations of momentum conserved and kinetic energy associated with some energy loss.

A common example of a perfectly inelastic collision is when two snowballs collide and then stick together afterwards. This equation describes the conservation of momentum:

$m_1 \mathbf u_{1} + m_2 \mathbf u_{2} = \left( m_1 + m_2 \right) \mathbf v\,$

It can be shown that a perfectly inelastic collision is one in which the maximum amount of kinetic energy is converted into other forms. For instance, if both objects stick together after the collision and move with a final common velocity, one can always find a reference frame in which the objects are brought to rest by the collision and 100% of the kinetic energy is converted. This is true even in the relativistic case and utilized inparticle accelerators to efficiently convert kinetic energy into new forms of mass-energy (i.e. to create massive particles).

Coefficient of restitution

Main article: Coefficient of restitution

The coefficient of restitution is defined as the ratio of relative velocity of separation to relative velocity of approach. It is a ratio hence it is a dimensionless quantity. The coefficient of restitution is given by:

$C_R = \frac{v_2 - v_1}{u_1 - u_2}$

for two colliding objects, where

v₁ is the scalar final velocity of the first object after impact,

v₂ is the scalar final velocity of the second object after impact,

u₁ is the scalar initial velocity of the first object before impact,

u₂ is the scalar initial velocity of the second object before impact.

A perfectly elastic collision implies that C_R is 1. So the relative velocity of approach is same as the relative velocity of separation of the colliding bodies.

Inelastic collisions have (C_R < 1). In case of a perfectly inelastic collision the relative velocity of separation of the centre of masses of the colliding bodies is 0. Hence the bodies stick together after collision.

Explosions

An explosion occurs as a result of a chain reaction that transforms potential energy into kinetic energy displacing the surrounding material. Explosions do not conserve potential energy. Instead, potential energy stored in chemical, mechanical, or nuclear form, is transformed into kinetic energy, acoustic energy, and electromagnetic radiation.

See the inelastic collision page for more details.

Modern definitions of momentum

Momentum in relativistic mechanics

In relativistic mechanics, in order to be conserved, the momentum of an object must be defined as

$\mathbf{p} = \gamma m_0\mathbf{v}\,,$

where m₀ is the invariant mass of the object and γ is the Lorentz factor, given by

$\gamma = \frac{1}{\sqrt{1 - (v/c)^2}}\,,$

where v is the speed of the object and c is the speed of light. The inverse relation is given by:

$\mathbf{v} = \frac{c^2 \mathbf{p}}{\sqrt{(pc)^2 + (m_0 c^2)^2}} = \frac{c^2 \mathbf{p}}{E} \,,$

where $p = \sqrt{p_x^2 + p_y^2 + p_z^2}$ is the magnitude of the momentum.

Relativistic momentum can also be written as invariant mass times the object's proper velocity, defined as the rate of change of object position in the observer frame with respect to time elapsed on object clocks (i.e. object proper time). Within the domain of classical mechanics, relativistic momentum closely approximates Newtonian momentum: at low velocity, γm₀v is approximately equal to m₀v, the Newtonian expression for momentum.

A graphical representation of the interrelation of relativistic energy E, invariant mass m₀, relativistic momentum p, and relativistic mass m = γm₀.

The total energy E of a body is related to the relativistic momentum p by

$E^2 = (pc)^2 + (m_0c^2)^2\,,$

where p denotes the magnitude of p. This relativistic energy-momentum relationship holds even for massless particles such as photons; by setting m₀ = 0 it follows that

$E = pc\,.$

For both massive and massless objects, relativistic momentum is related to the de Broglie wavelength λ by

$p = h/\lambda\,,$

where h is the Planck constant.

Four-vector formulation

Relativistic four-momentum as proposed by Albert Einstein arises from the invariance of four-vectors under Lorentzian translation. The four-momentum P is defined as:

$\mathbf{P} := (E/c, p_x , p_y ,p_z)\,,$

where E = γm₀c² is the total relativistic energy of the system, and p_x, p_y, and p_z represent the x-, y-, andz-components of the relativistic momentum, respectively.

The magnitude ||P|| of the momentum four-vector is equal to m₀c, since

$||\mathbf{P}||^2 = (E/c)^2 - p^2 = (m_0c)^2\,.$

which is invariant across all reference frames. For a closed system, the total four-momentum is conserved, which effectively combines the conservation of both momentum and energy into a single equation. For example, in the radiationless collision of two particles with rest masses

m 1

and

m 2

with initial velocities $\mathbf{v}_1$ and $\mathbf{v}_2$ , the respective final velocities $\mathbf{v}_3$ and $\mathbf{v}_4$ may be found from the conservation of four-momentum which states that:

$\mathbf{P}_1+\mathbf{P}_2=\mathbf{P}_3+\mathbf{P}_4\,,$

where

$\mathbf{P}_i=m_i\gamma_i(c,\mathbf{v}_i).$

For elastic collisions, the rest masses remain the same (

m 1 = m 3

and

m 2 = m 4

), while for inelastic collisions, the rest masses will increase after collision due to an increase in their heat energy content. The conservation of four-momentum can be shown to be the result of the homogeneity of space–time.

Generalization of momentum

Momentum is the Noether charge of translational invariance. As such, not just particles, but fields and other things can have momentum. However, where space–time is curved there is no Noether charge for translational invariance.

Momentum in quantum mechanics

Further information: Momentum operator

In quantum mechanics, momentum is defined as an operator on the wave function. The Heisenberg uncertainty principle defines limits on how accurately the momentum and position of a single observable system can be known at once. In quantum mechanics, position and momentum are conjugate variables.

For a single particle described in the position basis the momentum operator can be written as

$\mathbf{p}={\hbar\over i}\nabla=-i\hbar\nabla\,,$

where ∇ is the gradient operator, ħ is the reduced Planck constant, and i is the imaginary unit. This is a commonly encountered form of the momentum operator, though the momentum operator in other bases can take other forms, for example in the momentum basis the momentum operator is represented as

$\mathbf{p}\psi(p) = p\psi(p)\,,$

where the operator p acting on a wave function ψ(p) yields that wave function multiplied by the value p, in an analogous fashion to the way that the position operator acting on a wave function ψ(x) yields that wave function multiplied by the value x.

Momentum in electromagnetism

Electric and magnetic fields possess momentum regardless of whether they are static or they change in time. The pressure, P, of an electrostatic (magnetostatic) field upon a metal sphere, cylindrical capacitor or ferromagnetic bar is:

$P_{static} = {W}= \left[ {\epsilon_0 \epsilon}{\frac{{\mathbf E}^2 }{ {2}}} +{\frac{ 1 }{ {\mu_0 \mu} }} {\frac{{\mathbf B}^2}{{2}}} \right]\,,$

where ${W}\,$ , ${\mathbf E}\,$ , ${\mathbf B}\,$ , are the electromagnetic energy density, electric field, and magnetic field respectively. The electromagnetic pressure ${P}={W}\,$ may be sufficiently high to explode the capacitor. Thus electric and magnetic fields do carry momentum.

Light (visible, UV, radio) is an electromagnetic wave and also has momentum. Even though photons (the particle aspect of light) have no mass, they still carry momentum. This leads to applications such as the solar sail. The calculation of the momentum of light within dielectric media is somewhat controversial (see Abraham–Minkowski controversy).

Momentum is conserved in an electrodynamic system (it may change from momentum in the fields to mechanical momentum of moving parts). The treatment of the momentum of a field is usually accomplished by considering the so-called energy-momentum tensor and the change in time of the Poynting vector integrated over some volume. This is a tensor field which has components related to the energy density and the momentum density.

The definition of canonical momentum corresponding to the momentum operator of quantum mechanics when it interacts with the electromagnetic field is, using the principle of least coupling:

$\mathbf P = m\mathbf v + q\mathbf A\,$ ,

instead of the customary

$\mathbf p = m\mathbf v\,,$

where:

$\mathbf A\,$ is the electromagnetic vector potential

$m\,$ the charged particle's invariant mass

$\mathbf v\,$ its velocity

$q\,$ its charge.

Momentum with Examples

MOMENTUM

Look at the given pictures. If both the car and the truck have same speed, which one can be stopped first? Of course all you say, it is hard to stop truck relative to car. Well, what is the reason making car stop easier? They have same speed but different masses. Can mass effect the stopping time or distance? The answer is again YES! It is hard to stop heavier

objects. What we are talking about so far is momentum.

Momentum is a physical concept that is defined as “moving body”. In other words for talking about momentum momentum image1

we must have moving object, it must have both mass and velocity. Let me formulize what we said;

Momentum=Mass X Velocity

We show momentum in physics with “p”, mass with “m” and velocity with “v”. Then equation becomes;

p=m.v

Since velocity is a vector quantity and multiplied with mass (scalar quantity) momentum becomes also vector quantity. It has both magnitude and direction. Direction of momentum is the same as velocity. From the definition and given equation we can change momentum by changing its mass or changing its velocity.

Unit of the momentum is kg.m/s as you can guess from the equation.

Example Calculate the momentum of the give objects.

A basketball ball having 2kg mass and 6m/s velocity moves to the east
A car having 15m/s velocity and 1500kg mass moves to the north
A child having mass 25kg and velocity 2m/s moves to the west

a. Momentum of basketball;

b. Momentum of car;

c. Momentum of boy;

Lunes, Nobyembre 14, 2011

Impulse and Momentum

Impulse (physics)

Mathematical derivation in the case of an object of constant mass

Variable mass

Impulse and Newtons laws

Table Top Physics - Snooker/pool - left side

Method 1

Method 2

Which is correct?

Calculating motion from impulse

Physics - Dynamics - Collision response

Combined Rotation and Movement with a Linear Motion

Results

Collision Response for unconstrained rigid bodies

Physics Assumptions

Implementing this in program

Determining the impact point

Linear motion

Rotation motion

6 x 6 Matrix representation

Impulse with Examples

Momentum

Linear momentum of a particle

Linear momentum of a system of particles

Relating to mass and velocity

Relating to force – General equations of motion

Conservation of linear momentum

Elastic collisions

In one dimension

In multiple dimensions

Perfectly inelastic collisions

Coefficient of restitution

Explosions

Modern definitions of momentum

Momentum in relativistic mechanics

Four-vector formulation

Generalization of momentum

Momentum in quantum mechanics

Momentum in electromagnetism

Momentum with Examples